Squirmbag, Whale, Leviathan　が　X-wing, Swordfish, Jellyfish　で解釈できることの説明
（五，六，七人の賢い見張兵排除　が　二，三，四人の賢い見張兵排除　で解釈できることの説明）

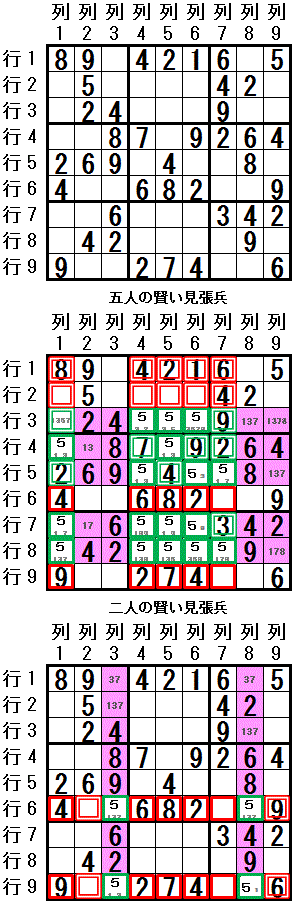左図で　数字５　について検討します。
（数字５　はすでに　行１列９，行２列２　に　２つ　配置されています）

まん中の図を見ると，
数字５　は，行３，行４，行５，行７，行８（base sets）では，列１，列４，列５，列６，列７（cover sets）以外のマスに　配置できないことがわかります。 Squirmbag（五人の賢い見張兵排除）です。
数字５　は，列１，列４，列５，列６，列７（cover sets）では，行３，行４，行５，行７，行８（base sets）以外の行の　赤いマス　には配置できません。
数字５　が配置できないマスのうち　行１，行２　の 赤い二重枠のマス　に　数字５　が配置できないことは，五人の賢い見張兵排除を利用しなくても　数字５　がすでに　行１列９，行２列２　に配置されていることからわかっています。
新たに　数字５　が配置できないことがわかったマスは，行６，行９の赤いマス（行６列１，行６列４，行６列５，行６列６，行６列７，行９列１，行９列４，行９列５，行９列６，行９列７）です（すでに数字が配置されているマスもあります）。

これを列で検討します。一番下の図を見ます。
数字５　は，列３，列８（base sets）では，行６，行９（cover sets）以外のマス　には配置できません。 X- wing（二人の賢い見張兵排除）です。
数字５　は，行６，行９（cover sets）では，列３，列８（base sets）以外の列の　赤いマス　には　配置できません。
数字５　が配置できないマスのうち　列２，列９　の 赤い二重枠のマス　に配置できないことは，数字５　がすでに　行１列９，行２列２　に配置されていることからわかっています。
新たに　数字５　が配置できないことがわかったマスは，列１，列４，列５，列６，列７の赤いマス（行６列１，行６列４，行６列５，行６列６，行６列７，行９列１，行９列４，行９列５，行９列６，行９列７）です（すでに数字が配置されているマスもあります）。
Squirmbag（五人の賢い見張兵排除）を行に適応したときに排除されるマスと同じです。

　

すでに　ｎ個のマスで　配置が確定している数字に関しては，base sets が ｋ行で　cover sets が　ｋ列での　賢い見張兵排除（Ｆｉｓｈ　基本形）が成立すると， 同じ局面で　base sets が （９−ｎ−ｋ）列で　cover sets が　（９−ｎ−ｋ）行　での　賢い見張兵排除（Ｆｉｓｈ　基本形）が成立し，同じ数字が同じマスから排除されます。

すでに　ｎ個のマスで配置が確定している数字に関して，その数字が配置されている行を除いた行の名前を要素とする集合を　Ｂ_０　とします。属する要素の数は　（９−ｎ）個　になります。上の例では，数字５　は　すでに　行１，行２　に配置されているので，
Ｂ_０ ＝｛３，４，５，６，７，８，９｝
と　なります（属する要素の数は　７個）。
すでにその数字が配置されている列を除いた列の名前を要素とする集合を　Ｃ_０　とします。上の例では，数字５　は　すでに　列２，列９　に配置されているので，
Ｃ_０ ＝｛１，３，４，５，６，７，８｝
と　なります。

ｋ人の賢い見張兵排除の条件は，base sets に含まれる行の名前を要素とする集合を　Ｂ（要素の数は　ｋ個），cover sets に含まれる列の名前を要素とする集合を　Ｃ　として，

すべての　ｉ ∈ Ｂ，ｊ ∈／ Ｃ　に対して，行 ｉ 列 ｊ　にその数字を配置できない　･･･　�@

と　なります。
排除されるマスについては，

すべての　ｊ ∈ Ｃ，ｉ ∈／ Ｂ　に対して，行 ｉ 列 ｊ　にその数字を配置できない　･･･　�A

と　なります。
（∈　は　集合の要素である，集合に属する　ことを，　∈／　は　集合の要素でない，集合に属さない　ことを表します）
上の例では，
Ｂ ＝｛３，４，５，７，８｝，Ｃ ＝｛１，４，５，６，７｝
です。

Ｂ_０　を全体集合としたときの　Ｂ　の補集合（Ｂに含まれないＢ_０の要素の集合。要素の数は　（９−ｎ−ｋ）個）を　Ｂ　と記載します。
Ｃ_０　を全体集合としたときの　Ｃ　の補集合　を　Ｃ　と記載します。 上の例では，
Ｂ ＝｛６，９｝，Ｃ ＝｛３，８｝
と　なります。

ｉ ∈／ Ｂ　と　ｉ ∈ Ｂ， ｉ ∈／ Ｂ　と　ｉ ∈ Ｂ， ｊ ∈／ Ｃ　と　ｊ ∈ Ｃ， ｊ ∈／ Ｃ　と　ｊ ∈ Ｃ　は　同値です。
�@の　ｉ ∈ Ｂ，ｊ ∈／ Ｃ　は， ｉ ∈ Ｂ，ｊ ∈ Ｃ　さらに 　ｊ ∈ Ｃ，ｉ ∈／ Ｂ　と　同値です。�@は，

すべての　ｊ ∈ Ｃ，ｉ ∈／ Ｂ　に対して，行 ｉ 列 ｊ　にその数字を配置できない　･･･　�@’

と　同値になります。
�@’が成立するということは，Ｃ　の要素を列名とした列を base sets，Ｂ　の要素を行名とした行を cover sets とした　賢い見張兵排除　の条件が満たされるということになります （（９−ｎ−ｋ）人の賢い見張兵排除になります）。
この時に，排除されるマスについては，

すべての　ｉ ∈ Ｂ，ｊ ∈／ Ｃ　に対して，行 ｉ 列 ｊ　にその数字を配置できない　･･･　�A’

と　なります。
�A’の　ｉ ∈ Ｂ，ｊ ∈／ Ｃ　は 　ｉ ∈／ Ｂ，ｊ ∈ Ｃ　すなわち 　ｊ ∈ Ｃ，ｉ ∈／ Ｂ　と同値であり，�A’　は　�A　は同じ表現となります。
太字 で記載した命題が成立することがわかります。